शास्त्रीय संगीताविषयी आणि गणिताविषयी मालिका सुरू करण्याचे उद्दीष्ट हे आहे की काही अमूर्त सौंदर्य कल्पनांपर्यंत पोहोचण्याचा मार्ग सुकर व्हावा. सर्वसामान्यपणे शास्त्रीय संगीताप्रमाणेच गणिताविषयी मनात एक सूक्ष्म अढी असते पण दोन्ही समजल्यावर आंनंद होतो. गणिताविषयीच्या मालिकेत काही संकल्पना आणि काही कोडी अशी जाणीवपूर्वक रचना केली आहे जेणेकरून वाचायलाही गंमत येईल.
चला तर मग ! मुकेश थळी मास्तरांच्या गणिताच्या तासाला सगळ्यांनी पटापट पाटी-पेन्सील घेऊन या!
‘मोगरा फुलला’ या दालनातील इतर लेख वाचण्यासाठी येथे क्लिक करा.
– सुनंदा भोसेकर
गणित विषय फारच रंजक आहे. गणिताच्या प्रत्येक दालनात म्हणजे अंकगणित, बीजगणित, भूमिती; ह्या सर्वच क्षेत्रांत तर्काचे व अचूकतेचे एक विलक्षण सौंदर्य भरलेले आहे. त्याचे अवलोकन करणारा जाणकार रसिक मात्र पाहिजे.
हा साधा प्रश्न पाहा. 1 ते 100 या आकड्यांमध्ये एकच संख्या अशी आहे जी दुसऱ्या एका संख्येचा वर्ग (square) आहे व आणखी एका संख्येचा घन (cube) आहे. ती कोणती?
तर उत्तर – 64.
कारण 64 हा 8 चा वर्गआहे. 8×8 = 64
4 चा घन आहे. 4x4x4 = 64
हे झाले एक अगदी साधे कोडे. आता आपण एका कूट प्रश्नाकडे वळूया. अगदी गंमतीशीर.
जनगणना अधिकारी एका घरात गेला. त्याने कुटुंब सदस्यांची नावे लिहून घेतली. आई गणिताची शिक्षिका होती. अधिकाऱ्याने प्रत्येकाचे वय विचारले. ती म्हणाली, माझं वय 38. तुला जर मुलींची वयं जाणून घ्यायची असेल तर गणितातून कोडे घातले तर ते सोडवायला आवडेल का? जनगणना अधिकारी म्हणाला, ‘जरूर!’. कारण तोही गणिताचा चाहता, दर्दी होता. त्याने आव्हान स्वीकारले.
ती म्हणाली, ‘मला तीन मुली. त्या मुलींच्या वयांचा गुणाकार केला तर 36 येतो. कळलं?’
अधिकारी म्हणाला, ‘मी वय सांगू शकत नाही. आणखीन धागा द्या’.
ती म्हणाली, ‘ त्या तिघींच्या वयांची बेरीज 13 येते. आता तरी जमेल?’
अधिकाऱ्याने दोन मिनिटे विचार केला व म्हणाला, ‘आता एकच अंतिम हिंट द्या’.
आई म्हणाली, ‘माझी मोठी मुलगी बाहेर खेळायला गेली आहे’.
अधिकारी हसत म्हणाला, ‘बस्स! झालं. तुमच्या मुलींची वयं आहेत, 9,2,2.
गुणाकार 36 होतो, बेरीज 13 होते.
इथे गंमत म्हणजे तिसरा धागा व दुसरा धागा. तीन मुलींच्या वयांचा गुणाकार म्हटल्याबरोबर त्या अधिकाऱ्याने विविध शक्यता लिहून काढल्या. गुणाकार 36 येतो अशा सात शक्यता होत्या. म्हणून त्याने आणखी एक धागा मागितला.
9 x 2 x 2
3 x 3 x 4
18 x 2 x 1
6 x 6 x 1
4 x 9 x 1
6 x 2 x 3
4 x 3 x 3
आई म्हणाली, त्यांच्या वयांची बेरीज 13. या धाग्याशी सातपैकी दोनच शक्यता जुळतात हे अधिकाऱ्याच्या लक्षात आले.
9, 2, 2 आणि 6, 6, 1.
यांची बेरीज 13 येते. पहिल्या शक्यतेमध्ये दोन वर्षांच्या जुळ्या मुली येत होत्या आणि दुसऱ्या शक्यतेमध्ये सहा वर्षाच्या. म्हणून त्याला आणखी एक हिंट घ्यावी लागली. मोठी मुलगी खेळायला गेली आहे, म्हणजे प्रश्न मिटला. मोठी एकच 9 वर्षांची. दोन बहिणी जुळ्या – 2, 2 वर्षांच्या. गणित अशा प्रकारे मनोरंजनात्मक रीतीनेही शिकवता येते.
आता आणखी थोडा कठीण कूटप्रश्न. हा प्रश्न बऱ्याच वर्षांपूर्वी आयआयटी जेईई म्हणजे संयुक्त प्रवेश परीक्षेत विचारला गेला होता. प्रश्न असा होता:
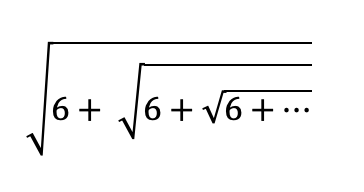
त्याचे उत्तर असे:

(वरचे एक मूळ काढले तरी आत राहते ते x. कारण ते अनंत)
𝓍2 = 6 + 𝓍 हे साधे समीकरण सोडवा.
𝓍2 – 𝓍 – 6 = 0
(𝓍 – 3) (𝓍 + 2) = 0
𝓍 = 3 or 𝓍 = (-2)
(-2) हे उत्तर होऊच शकत नाही, म्हणून 𝓍 = 3 हे उत्तर होय.
फिबोनाची या गणितज्ञाने गणिताच्या विविध क्षेत्रांत महत्त्वाची आणि मोलाची भर घातली आहे. त्याचा उपयोग अनेक क्षेत्रांत होतो. फिबोनाची क्रम (Fibonacci sequence) ही संख्यांची एक मालिका आहे. त्यामध्ये प्रत्येक संख्या ही आधीच्या दोन संख्यांची बेरीज असते, सामान्यतः 0 आणि 1 ने सुरू होते. पिसाचे इटालियन गणितज्ञ लिओनार्डो यांच्या नावावरून हे नाव देण्यात आले आहे, जे फिबोनाची म्हणून ओळखले जात होते. हा क्रम बऱ्याचदा विविध नैसर्गिक घटनांमध्ये दिसून येतो आणि त्याचा वापर संगणक विज्ञान, गणित आणि अगदी कलेतही होतो. तात्पर्य, प्रज्ञा आणि प्रतिभेच्या विविध निर्मिती व सृजन व्यापारात त्याचा उपयोग होतो.
फिबोनाची क्रम असा होतो:
0,1,1,2,3,5,8,13,21,34,55,89,144,…
या क्रमवारीत अमूक क्रमांकाची संख्या म्हणजे ‘n’th number शोधून काढायचा असल्यास त्याच्यासाठी सूत्र (formula) सुद्धा आहे.
तथापि, गणितात रंजकतेचे जे वैविध्य आहे, ते पाहून मन आश्चर्यचकित व आनंदित होते. भूमितीत त्रिकोण आणि चौकोन यांच्यावर आधारित कूटप्रश्न काही वेळा मेंदूला आव्हान स्वरूप असतात. विशेष करून स्पर्धात्मक परीक्षेत बुध्दिमत्ता चाचणीत सोपा वाटणारा प्रश्न तसा नसतो. चार उत्तरे तेथे दिलेली असूनही परीक्षार्थी अडचणीत येऊ शकतो, चुकू शकतो. अशा स्पर्धेत प्रश्नपत्रिका सोडवण्यासाठी वेळ मर्यादित असतो. हा प्रश्न पाहा.
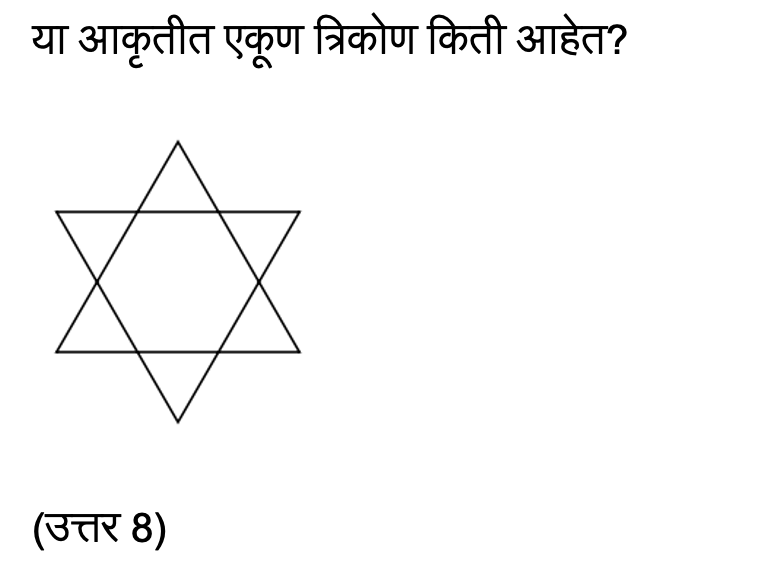

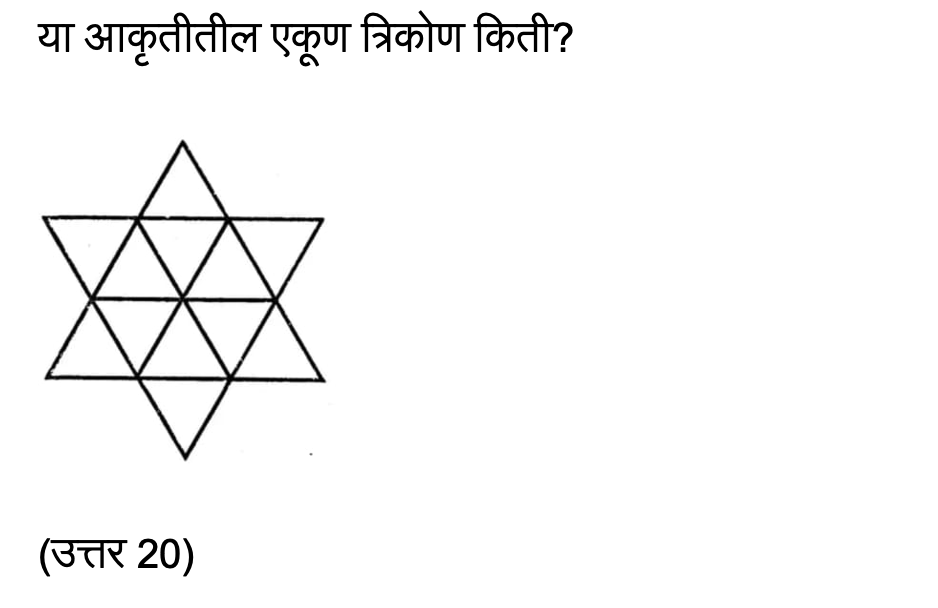
हंगेरीयन वंशाचे अमेरिकन गणितज्ञ पॉल हॉल्मोस यांनी गणितात मौलिक भर घातली आहे. त्यांची ख्याती कठीण संकल्पना आत्यंतिक सोप्या करण्याविषयी होती. त्यांनी म्हटलेच आहे, The only way to learn mathematics is to do mathematics. अर्थ – गणित शिकायचा एकमेव मार्ग म्हणजे गणिते सोडवणे. किती उचित आहे ही उक्ती!
शेवटी, तार्किक अधिष्ठानावर आधारित एक किंचित अवघड कोडे देतो. एका नाणी तयार करण्याच्या कारखान्यात टाकसाळीत दहा ग्रॅम वजनाची नाणी तयार करत असत. एका पाईपवर रांगेत दहा छिद्रे होती, त्यातून धडाधड नाणी खालच्या मोठाल्या टबमध्ये पडायची. तेथे टब होते. अचानक व्यवस्थापकाच्या लक्षात आले, की फक्त एका टबमध्ये सगळी नाणी 9 ग्रॅमची पडत आहेत. त्याने एका कुशल इंजिनीयरला बोलावले. त्याला सांगितले, की कुठल्या टबात डिफेक्टिव म्हणजे 9 ग्रॅम वजनाची नाणी पडत आहेत ते शोधायचे आहे. प्रत्येक टबमधून एकेक नाणे काढून, त्याचे वजन करून हे शोधणे सोपे आहेच. पण वेळ जाईल. वजन करण्याचा फक्त एक प्रयत्न करून कुठल्या टबमध्ये डिफेक्टिव नाणी पडत आहेत ते सांगावे. मी ते युनिट व ते काम बंद करतो. हा घ्या डिजिटल वजन मापक. सगळ्या टबांतील पाहिजे तितकी नाणी घ्या. पण एकदा वजनमापकावर ठेवली की प्रयत्न संपला.
इंजिनीयरने एक मिनिट विचार केला आणि डिफेक्टिव नाणी कुठल्या टबमध्ये आहे हे सांगितले. गंमत पाहा. हुशार इंजिनीयरने वर सांगितले:
‘50, 100 किंवा त्यापेक्षाही जास्त टब असले तरीही एका प्रयत्नात डिफेक्टिव नाण्यांचे टब शोधून काढणे अगदी सहज शक्य आहे.’ गणितप्रेमी अभ्यासकहो, आपण हे करू शकाल का? याचे उत्तर या स्तंभाखालच्या कमेंट्समध्ये लवकरच देऊ. हा कूटप्रश्न कठीण नाही आणि सोपाही नाही.
गणिताची रूची, असोशी, आवड अशीच वृद्धिंगत होवो.
– मुकेश थळी 9545827662 anushanti561963@gmail.com





गणित विषयक मालिका वाचायला निश्चितच आवडेल, लेख प्रसिद्ध झाल्यास लिंक कुठे मिळेल.